21.3.7.2. Global Optimization Problem

Most of global optimization approaches requires stochastic process. Especially Genetic algorithm requires many sampling points. If one wants nearly global optimum, Latin hypercube sampling is recommended because it gives good space-filled sampling points. Lets’ consider the following global optimization problem.

\(\underset{\mathbf{x}\in \Omega }{\mathop{\min }}\,f\left( \mathbf{x} \right)={{\left( {{x}_{1}}{{x}_{2}} \right)}^{2}}+{{x}_{1}}x_{2}^{2}-3{{x}_{1}}{{x}_{2}},\text{where }\Omega =\left\{ \left. \mathbf{x} \right|-3\le {{x}_{i}}\le 3,i=1,2 \right\}.\)

CASE 1: The number of initial sampling points is 15. Then, a multi-quadratics radial basis function is employed. As you can see, AutoDesign uses the best one of sampling points as the initial design point. So, it can easily go to an optimum while sampling points fill the design space properly. Figure 21.90 shows the initial sampling points (Blue) and 9 SAO ones (Red).

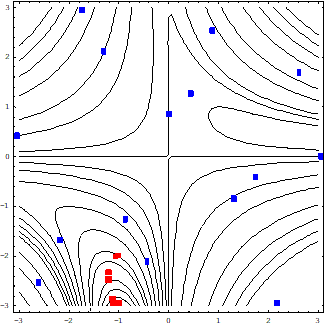
Figure 21.90 Case study 1: global optimization using RBF

CASE 2: In this case, Kriging model is used to solve the same optimization problem. For fair comparison, the same sampling points are used. Figure 21.91 shows the initial sampling points (Blue) and 10 SAO ones (Red). Although the SAO points are somewhat different from those of Case 1 study, this approach can successfully converge to the same optimum.

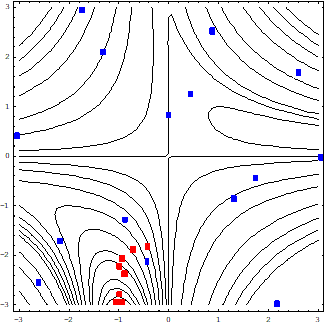
Figure 21.91 Case study 2: global optimization using Kriging