41.2.2. Slip Ratio & Friction

41.2.2.1. Longitudinal Slip Ratio

The longitudinal slip ratio, \(S\), is defined to be

(41.16)\[\begin{split}S=\left\{ \begin{matrix} 0<\frac{{{v}_{xcir}}}{{{v}_{x}}}<1\text{ during braking} \\ -1<\frac{{{v}_{xcir}}}{{{v}_{cir}}}<0\text{ during traction} \\ \end{matrix} \right.\end{split}\]

The absolute value of longitudinal slip ratio, \({{S}_{s}}\), is therefore:

(41.17)\[{{S}_{s}}=\left| s \right|\]

41.2.2.2. Lateral Slip Ratios

The slip angle \(\alpha\) is defined as:

(41.18)\[\alpha ={{\tan }^{-1}}({{v}_{y}},\text{ }{{v}_{x}})\]

The lateral slip ratio due to slip angle, \({{S}_{\alpha }}\), may then be defined as:

(41.19)\[\begin{split}{{{S}'}_{\alpha }}=\left\{ \begin{matrix} \left| \tan \alpha \right|=\left| \frac{{{v}_{y}}}{{{v}_{x}}} \right| & \text{during braking} \\ (1-{{S}_{s}})\left| \tan \alpha \right|=\left| \frac{v{}_{y}}{{{v}_{cir}}} \right| & \text{during traction} \\ \end{matrix} \right.\end{split}\]

The lateral slip ratio due to inclination angle, \({{S}_{\gamma }}\), is defined as:

(41.20)\[{{S}_{\gamma }}=\left| \sin \gamma \right|\]

A combined lateral slip ratio due to slip and inclination angles, \({{S}_{\alpha \gamma }}\), is defined as:

(41.21)\[\begin{split}{{{S}'}_{\alpha \gamma }}=\left\{ \begin{matrix} \left| \tan \alpha -\frac{\ell \sin \gamma }{2{{r}_{1}}} \right| & \text{during braking} \\ \left| (1-{{S}_{s}})\tan \alpha -\frac{\ell \sin \gamma }{2{{r}_{1}}} \right| & \text{during traction} \\ \end{matrix} \right.\end{split}\]

where, \(\ell \approx \sqrt{8{{r}_{1}}(delta)}\) is the length of the contact patch.

41.2.2.3. Comprehensive Slip Ratio

A comprehensive slip ratio due to slip ratio, slip angle, and inclination angle may be defined as:

(41.22)\[{{{S}'}_{s\alpha \gamma }}=\sqrt{{{S}_{s}}^{2}+{{S}_{\alpha \gamma }}^{2}}\]

Note that:

\({{S}_{s\alpha \gamma }}={{S}_{s}}\) for \(\alpha =\gamma =0\)

\({{S}_{s\alpha \gamma }}={{S}_{\alpha }}\) for \(s=\gamma =0\)

\({{S}_{s\alpha \gamma }}={{S}_{\gamma }}\) for \(s=\alpha =0\)

\({{S}_{s\alpha \gamma }}={{S}_{\alpha \gamma }}\) for \(s=0\)

Now a slip velocity directional angle:math:beta may be defined as:

(41.23)\[\beta ={{\tan }^{-1}}\left( {{S}_{\alpha \gamma }},\text{ }{{\text{S}}_{\text{s}}} \right)\]

41.2.2.4. Friction Models in the TIRE Statement

In the Tire statement, a linear relationship between \({{S}_{s\alpha \gamma }}\) and \(\mu\), the corresponding road-tire friction coefficient, is assumed.

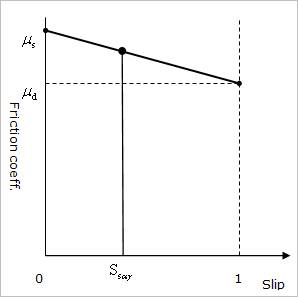
Figure 41.9 Linear Friction Model

(41.24)\[\mu ={{\mu }_{s}}-({{\mu }_{s}}-{{\mu }_{d}}) \times {{S}_{s\alpha \gamma }}\]

\({{\mu}_{s}}\): Static Friction Coefficient

\({{\mu}_{d}}\): Dynamic Friction Coefficient

The friction circle concept allows for different values of longitudinal and lateral friction coefficients(\({{\mu }_{x}}\) and \({{\mu }_{y}}\)) but limits the maximum value for both coefficients to \(\mu\).

The relationship that defines the friction circle follows:

(41.25)\[{{\left( \frac{{{\mu }_{x}}}{\mu } \right)}^{2}}+{{\left( \frac{{{\mu }_{y}}}{\mu } \right)}^{2}}=1\]

or \({{\mu }_{x}}=\mu \cos \theta\)

and \({{\mu }_{y}}=\mu \sin \theta\)

where, \(\cos \theta =\frac{{{S}_{s}}}{{{{{S}'}}_{s\alpha \gamma }}}\)

The Fiala tire model uses only \(\mu\) and not \({{\mu }_{x}}\) and \({{\mu }_{y}}\). The UATIRE model uses \(\mu\), \({{\mu }_{x}}\), and \({{\mu }_{y}}\).