21.3.9.4. Interpretation of SAO based Hybrid Method Results
We provide two result sheets such as Result Sheet and Summary Sheet. Figure 21.123 shows Result Sheet. The 1st iteration results shows \(AR\approx 36\) and Reliability Index \(Error\approx 0\). Then, only 2 iterations are required to solve the reliability analysis problem. It is noted that two errors of the final iteration meet zero.
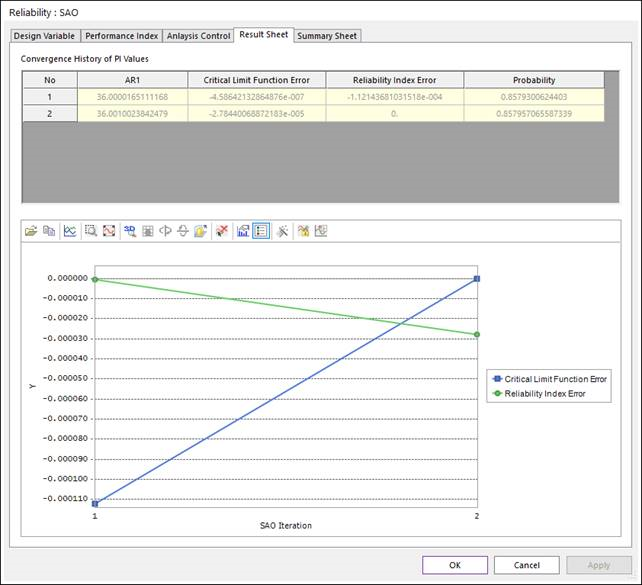
Figure 21.123 Result Sheet of SAO method
Next, we explains Summary Sheet. First, it lists Statistical Information. As explained in the interpretation of Monte-Carlo simulation, Table 1 summarized the statistical parameters (Param_1 ~ Param_3). Next, let see Performance index (Result). AFORM+DRM1 gives ‘Reliability Index = #.1467* and Failure Probability = 0.8742.
From the view point of robust design and 6-sigma design, one can regard the reliability index (\(\beta\)) as ‘k-sigma’ conceptually. Also, it can be the distance from Mean value to MPP (Most Probable Point). MPP is the nearest point on hyper-surface (PI=0) from mean value in the normalized space. Thus, finding the reliability index is ‘constrained optimization problem’.

Figure 21.124 Summary Sheet of SAO method
In Most Probable Point Information, MPP_DV is re-transformed into the original DV space. Thus, the value of two-norm between Mean and MPP_DV becomes Reliability Index. Next, let’s consider the design sensitivity information such as D(Beta)/D(Mean), D(Beta)/D(STDV), D(P)/D(Mean), and D(P)/D(STDV). These values are the derivatives of Reliability Index and Failure Probability with respect to Mean and Standard deviation.
Let’s consider two cases in Figure 21.125 and Figure 21.126. Suppose that mean value (\({{\mu }_{1}},{{\mu }_{2}}\)) moves into (\({{\mu }_{1}}+{{\Delta }_{1}},{{\mu }_{2}}+{{\Delta }_{2}}\)) along the axis. Then, how much is reliability index changed? The design sensitivity D(Beta)/D(Mean) is the change rate of reliability index.
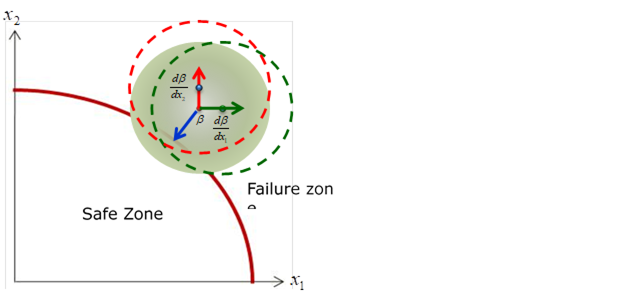
Figure 21.125 In case that ‘Mean point’ is in failure zone [Graphical representation of D(Beta)/D(Mean)]
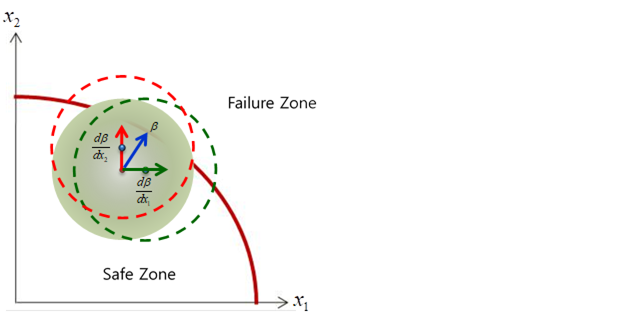
Figure 21.126 In case of ‘Mean point is in safe zone [Graphical representation of D(Beta)/D(Mean)]
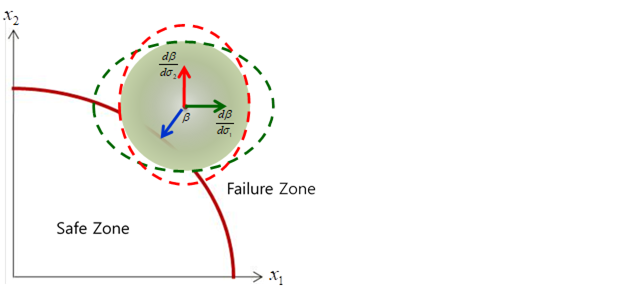
Figure 21.127 In case that ‘Mean point’ is in failure zone Graphical representation of D(Beta)/D(STDV)
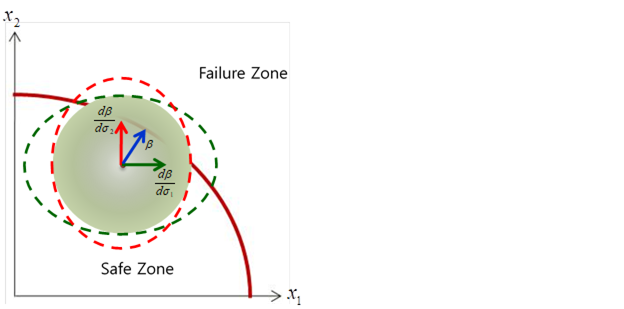
Figure 21.128 In case of ‘Mean point is in safe zone [Graphical representation of D(Beta)/D(STDV)]
Figure 21.127 and Figure 21.128 show the graphical representation of D(Beta)/D(STDV). This represents the change rate of reliability index when the standard deviation \(({{\sigma }_{1}},{{\sigma }_{2}})\) is increase by \((\sigma {}_{1}+{{\Delta }_{1}},\sigma {}_{2}+{{\Delta }_{2}})\).
Similarly, the values of D(P)/D(Mean) and D(P)/D(STDV) represent the change rate of failure probability when the mean value moves and the standard deviation is increased. These design sensitivity information is used to estimate the reliability index** and failure probability.
By substituting the analysis results shown in Figure 21.127 and Figure 21.128, the failure probability can be estimated by using the follow approximation form.
\(\begin{aligned} & \tilde{P}=P+\sum{\frac{\partial P}{\partial {{\mu }_{i}}}}\left( \Delta {{\mu }_{i}} \right)+\sum{\frac{\partial P}{\partial {{\sigma }_{i}}}}\left( \Delta {{\sigma }_{i}} \right) \\ & =0.857+0.15639\Delta {{\mu }_{1}}+0.15639\Delta {{\mu }_{2}}-0.1184\Delta {{\sigma }_{1}}-0.1184\Delta {{\sigma }_{2}} \end{aligned}\)
In order to help one’s understand, we solve the reliability analysis problem shown in Figure 21.129. The mean value lies in safe zone. Also, \({{\mu }_{1}}\) and \({{\mu }_{2}}\) are different values.

Figure 21.129 Reliability analysis in case that ‘mean value’ lies in safe zone.
Figure 21.130 shows the summary sheet of reliability analysis results. The failure probability is 1.09(%). The design sensitivity information explains that DP2 (\({{x}_{2}}\))is more sensitive to failure than DP1.
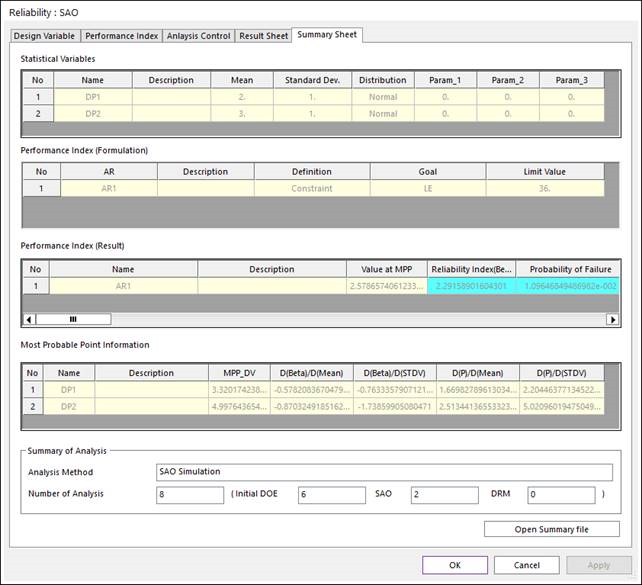
Figure 21.130 Summary Sheet of the reliability analysis problem shown in Figure 21.125 and Figure 21.126