10.1.1. Equations of Motion using Modal Approach
Kinematics
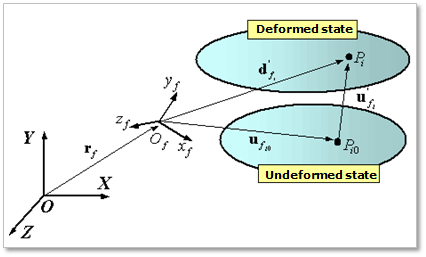
Figure 10.2 Configuration of a flexible body
Figure 10.2 shows the configuration of a flexible body \(f\) in the undeformed and deformed state. In the figure,
\(XYZ\) : Inertia reference frame
\(O\) : Origin of XYZ
\({{x}_{f}}{{y}_{f}}{{z}_{f}}\) : Flexible body reference frame
\({{O}_{f}}\) : Origin of \({{x}_{f}}{{y}_{f}}{{z}_{f}}\)
\({{P}_{i0}}\) : Node \(i\) in the undeformed state
\({{P}_{i}}\) : Node \(i\) in the deformed state
\({{r}_{f}}\) : Position vector from the point \(O\) to the point \({{O}_{f}}\)
\({\mathbf{u}_{{f}_{i0}}}\) : Position vector from the point \({{O}_{f}}\) to the \({{P}_{i0}}\)
\(\mathbf{u}_{{f}_{i}}^{'}\) : Nodal elastic deformation position vector from the point \({{P}_{i0}}\) to the \({{P}_{i}}\) measured with respect to \({{x}_{f}}{{y}_{f}}{{z}_{f}}\). \(\mathbf{u}_{{{f}_{i}}}^{'}\) is nodal elastic deformation
\(\mathbf{d}_{{{f}_{i}}}^{'}\) : \(\mathbf{u}_{{{f}_{i0}}}+\mathbf{u}_{{{f}_{i}}}^{'}\), position vector from the point \({{O}_{f}}\) to the point \({{P}_{i}}\)
For a generic node \(i\) of a flexible body \(f\), position vector of the node can be written as
where,
In above equation, \(\boldsymbol\Phi_{T}^{{{f}_{1}}}\) is the translational modal matrix of a node \(i\).
By taking time differentiation of the position vector, velocity of the node \(i\) is obtained as follows;
By taking time differentiation of the velocity vector, acceleration of the node \(i\) is obtained as follows;
where,
EOM
By the virtual work principle, equations of motion can be obtained as
\(\mathbf{B}^{T}\left( \mathbf{M}\begin{Bmatrix} \dot{\mathbf{Y}} \\ \ddot{\mathbf{a}} \end{Bmatrix} + \mathbf{C}_{\mathbf{z}_c}^{T} \boldsymbol{\lambda}_1 -\mathbf{Q}^C -\mathbf{Q}^E-\mathbf{Q}^G -\mathbf{Q}^D -\mathbf{Q}^F \right) + \mathbf{C}_{\mathbf{q}_c}^{T}\boldsymbol{\lambda}_2 -\mathbf{Q}^J = 0\)
- where,
- \(\mathbf{z}:\text{ Cartesian coordinates}\text{.}\)\(\mathbf{a}:\text{ Modal coordinates}\text{.}\)\(\mathbf{q}:\text{ Relative coordinates}\text{.}\)\(\mathbf{M}\text{=}\left[ \begin{matrix} {{\mathbf{M}}_{zz}} & {{\mathbf{M}}_{za}} \\ {{\mathbf{M}}_{az}} & {{\mathbf{M}}_{aa}} \\ \end{matrix} \right]:\text{ Mass matrix}\text{.}\)\(\dot{\mathbf{Y}}:\text{ Local acceleration of cartesian coordinates}\text{.}\)\(\mathbf{C}_{\mathbf{z}_{c}}^{{}}:\text{ Partial derivative terms of constraint equations with respect to }{{\mathbf{z}}_{c}}\text{.}\)\(\mathbf{C}_{\mathbf{q}_{c}}^{{}}:\text{ Partial derivative terms of constraint equations with respect to }{{\mathbf{q}}_{c}}\text{.}\)\(\boldsymbol{\lambda}_{1}:\text{ Lagrangian multipliers}\text{.}\)\(\boldsymbol{\lambda}_{2}:\text{ Lagrangian multipliers}\text{. (Driving constraint of a joint)}\)\(\mathbf{Q}_{{}}^{C}:\text{ Quadratic velocity term}\text{.}\)\(\mathbf{Q}_{{}}^{E}:\text{ Elastic force term}\text{.}\)\(\mathbf{Q}_{{}}^{G}:\text{ Gravitational force term}\text{.}\)\(\mathbf{Q}_{{}}^{D}:\text{ Damping force term}\text{.}\)\(\mathbf{Q}_{{}}^{F}:\text{ Etc}\text{. force terms}\text{. (Modal force, Generalized force, Contact force ...)}\)\(\mathbf{Q}_{{}}^{J}:\text{ Joint friction force term}\text{.}\)