40.3.2.1. Specification of MMS Type C (One-step, Two-step)

Simple diagram of One-step and Two-step spring

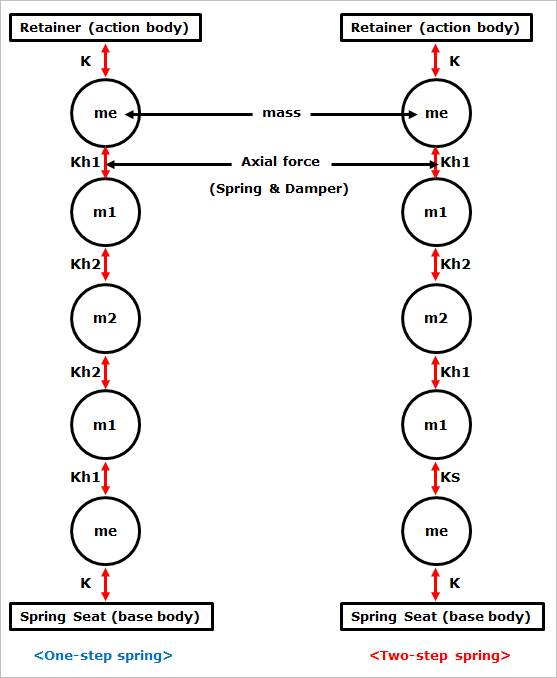
Figure 40.31 Simple diagram of One-step and Two-step spring

Internal Parameter

The internal parameters are calculated in Solver. It means that the user cannot confirm the internal parameters directly in GUI. However, the internal parameters can be confirmed in post processor using Request function in Subentity menu.

• Stiffness for fully contact:

  \[\begin{flalign} & K\left( {N}/{mm}\; \right)\ \ \ \ K=\frac{\pi DoE}{{{10}^{3}}}&& \end{flalign}\]

• Stiffness for free length:

  \[\begin{flalign} & {{K}_{1}}\left( N/mm\ \right)\ \ \ \ {{K}_{1}}=\frac{{G}'D{{w}^{4}}}{8\left( {{N}_{1}}+{{N}_{2}}-2{{N}_{b}} \right)D{{o}^{3}}}&& \end{flalign}\]

  \[\begin{flalign} & {{{{n}'}}_{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{{{n}'}}_{1}}=\frac{{{L}_{f}}-Dw\left( {{N}_{1}}+{{N}_{2}}-1 \right)}{\left( {{N}_{1}}+{{N}_{2}}-2{{N}_{b}} \right)Do}&& \end{flalign}\]

• Natural Frequency for free length:

  \[\begin{flalign} & {{f}_{1}}\left( Hz \right)\ \ \ \ \ \ \ \ \ {{f}_{1}}=\sqrt{\frac{{{G}'}}{2{\rho }'}}\frac{Dw}{2\pi \left( {{N}_{1}}+{{N}_{2}}-2{{N}_{b}}+{{{{n}'}}_{1}} \right)D{{o}^{2}}}&& \end{flalign}\]

• Total Mass of spring:

  \[\begin{flalign} & M\left( kg \right)\ \ \ \ \ \ \ \ \ \ M=\frac{{{\pi }^{2}}}{4}{\rho }'DoD{{w}^{2}}\left( {{N}_{1}}+{{N}_{2}}-0.7 \right)&& \end{flalign}\]

• Set-up load:

  \[\begin{flalign} & Pc\left( mm \right)\ \ \ \ \ \ \ \ Pc=\frac{2\left( Ls-Dw\left( {{N}_{1}}+{{N}_{2}}-1 \right) \right)}{{{N}_{2}}}&& \end{flalign}\]

  \[\begin{flalign} & Lc\left( mm \right)\ \ \ \ \ \ \ \ Lc=Dw\left( {{N}_{1}}+{{N}_{2}}+0.5 \right)&& \end{flalign}\]

  \[\begin{flalign} & Fset\left( N \right)\ \ \ \ \ \ \ \ Fset=\left( Lf-Ls \right){{K}_{1}}&& \end{flalign}\]

• Stiffness for set-up length:

  \[\begin{flalign} & {{K}_{2}}\left( {N}/{mm}\; \right)\ \ \ \ {{K}_{2}}=\frac{{G}'D{{w}^{4}}}{8\left( {{N}_{2}}-{{N}_{b}} \right)D{{o}^{3}}}\ \ \ \left[ for\ One\ step\ spring,\ {{K}_{2}}={{K}_{1}} \right]&& \end{flalign}\]

  \[\begin{flalign} & {{{{n}'}}_{2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\,{{{{n}'}}_{2}}=\frac{{{L}_{s}}-Dw\left( {{N}_{1}}+{{N}_{2}}-1 \right)}{\left( {{N}_{2}}-{{N}_{b}} \right)Do}&& \end{flalign}\]

• Natural frequency for set-up length:

  \[\begin{flalign} & {{f}_{2}}\left( Hz \right)\ \ \ \ \ \ \ \ \ {{f}_{2}}=\sqrt{\frac{{{G}'}}{2{\rho }'}}\frac{Dw}{2\pi \left( {{N}_{2}}-{{N}_{b}}+{{{{n}'}}_{2}} \right)D{{o}^{2}}}&& \end{flalign}\]

Model variable for One-Step spring

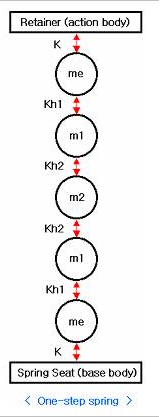
Figure 40.32 Model variable for One-Step spring

\[\begin{flalign} K{{h}_{1}}=\frac{16}{5}\cdot \frac{K{{K}_{1}}}{K-2{{K}_{1}}}&& \end{flalign}\]

\[\begin{flalign} K{{h}_{2}}=\frac{16}{3}\cdot \frac{K{{K}_{1}}}{K-2{{K}_{1}}}&& \end{flalign}\]

\[\begin{flalign} {{m}_{1}}=\frac{8}{15}\cdot \frac{1}{{{\pi }^{2}}f_{1}^{2}}\cdot \frac{K{{K}_{1}}}{K-2{{K}_{1}}}&& \end{flalign}\]

\[\begin{flalign} {{m}_{2}}=\frac{4}{9}\cdot \frac{1}{{{\pi }^{2}}f_{1}^{2}}\cdot \frac{K{{K}_{1}}}{K-2{{K}_{1}}}&& \end{flalign}\]

\[\begin{flalign} me=\frac{\left( M-2{{m}_{1}}-{{m}_{2}} \right)}{2}&& \end{flalign}\]

Model variable for Two-Step spring

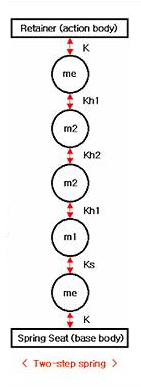
Figure 40.33 Model variable for Two-Step spring

\[\begin{flalign} & K{{h}_{1}}=\frac{8}{3}\cdot \frac{K{{K}_{2}}}{K-3{{K}_{2}}}&& \end{flalign}\]

\[\begin{flalign} K{{h}_{2}}=4\cdot \frac{K{{K}_{2}}}{K-3{{K}_{2}}}&& \end{flalign}\]

\[\begin{flalign} Ks=\frac{K{{K}_{1}}{{K}_{2}}}{K{{K}_{2}}+{{K}_{1}}{{K}_{2}}-K{{K}_{1}}}&& \end{flalign}\]

\[\begin{flalign} {{m}_{1}}=\frac{1}{\omega _{1}^{2}}\left\{ K{{h}_{1}}+Ks-\frac{Kh_{1}^{2}\left( K{{h}_{1}}+K{{h}_{2}}-{{m}_{2}}\omega _{1}^{2} \right)}{\left( K{{h}_{1}}+2K{{h}_{2}}-{{m}_{2}}\omega _{1}^{2} \right)\left( K{{h}_{1}}-{{m}_{2}}\omega _{1}^{2} \right)} \right\}\ \ \ \ where,\ {{\omega }_{1}}=2\pi {{f}_{1}}&& \end{flalign}\]

\[\begin{flalign} {{m}_{2}}=\frac{K{{h}_{1}}}{4{{\pi }^{2}}f_{2}^{2}}&& \end{flalign}\]

\[\begin{flalign} me=\frac{\left( M-2{{m}_{2}}-{{m}_{1}} \right)}{2}&& \end{flalign}\]

Nonlinear characteristics

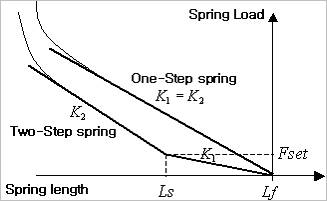
Figure 40.34 Characteristics of K1 and K2

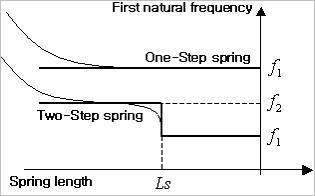
Figure 40.35 Characteristics of natural frequency

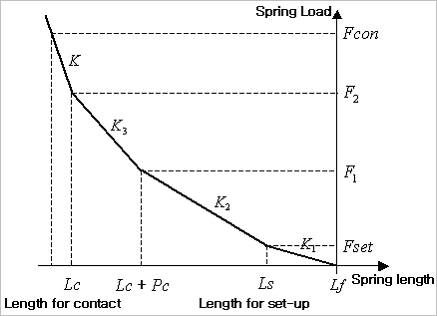
Figure 40.36 Characteristics of stiffness according to spring length

• Nonlinear characteristics

  \[\begin{flalign} {{F}_{1}}=Fset+\left( Ls-Lc-Pc \right){{K}_{2}}&& \end{flalign}\]

  \[\begin{flalign} {{K}_{3}}=1.15{{K}_{2}}&& \end{flalign}\]

  \[\begin{flalign} {{F}_{2}}={{F}_{1}}+Pc{{K}_{3}}&& \end{flalign}\]

  \[\begin{flalign} Fcon={{K}_{1}}\left( Lf-Ls \right)+{{K}_{2}}\left( Ls-Dw\left( {{N}_{1}}+{{N}_{2}}-0.5 \right) \right)&& \end{flalign}\]

• Nonlinear characteristics of \(Kh_1\) for One-Step and Two-Step spring

  \[\begin{flalign} {{x}_{11}}=\frac{F_1}{Kh_1}&& \end{flalign}\]
  \begin{flalign} {{Kh}_{1}}' &= {\frac{16}{5}} {\cdot} {\frac{KK_3}{K-2K_3}} \ \ \ \ :for\ One\_Step\ spring \\ &= {\frac{8}{3}} {\cdot} {\frac{KK_3}{K-3K_3}} \ \ \ \ :for\ Two\_Step\ spring && \end{flalign}

  Set \(x_{12}\) as follows

  \[\begin{flalign} {{x}_{12}}=\frac{F_2-F_1}{Kh_1} + {{x}_{21}}&& \end{flalign}\]
  \[\begin{split}\begin{flalign} \left[ \begin{matrix} {x}_{11}^2 & {x}_{11} & 1 \\ {x}_{12}^2 & {x}_{12} & 1 \\ {2x}_{11} & 1 & 0 \end{matrix} \right] & \cdot \left\{ \begin{matrix} {a}_{k1} \\ {b}_{k1} \\ {c}_{k1} \end{matrix} \right\} & = \left\{ \begin{matrix} F_1 \\ F_2 \\ Kh_1 \end{matrix} \right\} && \end{flalign}\end{split}\]

  Using this, \(a_{h1}\), \(b_{h1}\), and \(c_{h1}\) can be obtained.

  Set \(x_{13}\), \(Kh_{1c}\) and \(x_{14}\) as follows,

  \[\begin{flalign} {x}_{13}=\frac{1}{{2a}_{k1}} \left\{ {-b}_{k1}+\sqrt{{b}_{k1}^{2}-{4a}_{k1} ({c}_{k1}-{F}_{con})} \right\} && \end{flalign}\]
  \[\begin{flalign} {Kh}_{1c}={2a}_{k1}{x}_{13}+{b}_{k1} && \end{flalign}\]
  \[\begin{flalign} {x}_{14}={x}_{13}+\frac{Pc}{10} && \end{flalign}\]
  \[\begin{split}\begin{flalign} \left[ \begin{matrix} x_{13}^2 & X_{13} & 1 \\ x_{14}^2 & x_{14} & 1 \\ 2x_{13} & 1 & 0 \end{matrix} \right] \cdot \left\{ \begin{matrix} a_{k1c} \\ b_{k1c} \\ c_{k1c} \end{matrix} \right\} = \left\{ \begin{matrix} F_{con} \\ 2F_{con} \\ Kh_{1c} \end{matrix} \right\} && \end{flalign}\end{split}\]

  Using this, \(a_{hlc}\), \(b_{hlc}\), and \(c_{hlc}\) can be obtained.

  Spring load for \(Kh_{1}\) becomes as follows,

  \(F=Kh_{1} \cdot x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ : x < x_{11}\)

  \(F=a_{k1}x^2+b_{k1}x+c_{k1} \ \ \ \ \ \ : x_{11} \leq x < x_{13}\)

  \(F=a_{k1c}x^2+b_{k1c}x+c_{k1c} \ \ \ \ \ : x_{13} \leq x\)

  

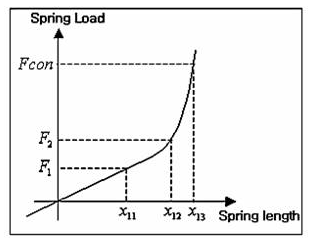
• Nonlinear characteristics of \(Kh_2\) for One-Step and Two-Step spring

  \[\begin{flalign} {{x}_{21}}=\frac{F_1}{Kh_2}&& \end{flalign}\]
  \begin{flalign} {{Kh}_{2}}' &= \frac{16}{3} \cdot \frac{KK_3}{K-2K_3} \ \ \ \ :for\ One\_Step\ spring \\ &= 4 \cdot \frac{KK_3}{K-3K_3}\ \ \ \ \ \ \ \ \ \ :for\ Two\_Step\ spring \end{flalign}

  Set \(x_{22}\) as follows

  \[\begin{flalign} {{x}_{22}}=\frac{F_2-F_1}{K-2K_3} + {{x}_{21}}&& \end{flalign}\]
  \[\begin{split}\begin{flalign} \left[ \begin{matrix} {x}_{21}^2 & {x}_{21} & 1 \\ {x}_{22}^2 & {x}_{22} & 1 \\ {2x}_{21} & 1 & 0 \end{matrix} \right] & \cdot \left\{ \begin{matrix} {a}_{k2} \\ {b}_{k2} \\ {c}_{k2} \end{matrix} \right\} & = \left\{ \begin{matrix} F_1 \\ F_2 \\ Kh_2 \end{matrix} \right\} && \end{flalign}\end{split}\]

  Using this, \(a_{h2}\), \(b_{h2}\), and \(c_{h2}\) can be obtained.

  Set \(x_{23}\), \(Kh_{1c}\) and \(x_{24}\) as follows,

  \[\begin{flalign} {x}_{23}=\frac{1}{{2a}_{k2}} \left\{ {-b}_{k2}+\sqrt{{b}_{k2}^{2}-{4a}_{k2} ({c}_{k2}-{F}_{con})} \right\} && \end{flalign}\]
  \[\begin{flalign} {Kh}_{2c}={2a}_{k2}{x}_{23}+{b}_{k2} && \end{flalign}\]
  \[\begin{flalign} {x}_{24}={x}_{23}+\frac{Pc}{10} && \end{flalign}\]
  \[\begin{split}\begin{flalign} \left[ \begin{matrix} {x}_{23}^2 & {X}_{23} & 1 \\ {x}_{24}^2 & {x}_{24} & 1 \\ {2x}_{23} & 1 & 0 \end{matrix} \right] & \cdot \left\{ \begin{matrix} {a}_{k2c} \\ {b}_{k2c} \\ {c}_{k2c} \end{matrix} \right\} & = \left\{ \begin{matrix} Fcon \\ 2Fcon \\ {Kh}_{2c} \end{matrix} \right\} && \end{flalign}\end{split}\]

  Using this, \(a_{h2c}\), \(b_{h2c}\), and \(c_{h2c}\) can be obtained.

  Spring load for \(Kh_{2}\) becomes as follows,

  \(F=Kh_{2} \cdot x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ : x < x_{21}\)

  \(F=a_{k2}x^2+b_{k2}x+c_{k2} \ \ \ \ \ \ : x_{21} \leq x < x_{23}\)

  \(F=a_{k2c}x^2+b_{k2c}x+c_{k2c} \ \ \ \ \ : x_{23} \leq x\)

  

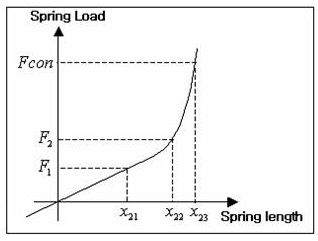
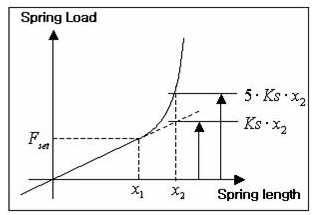
• Nonlinear characteristics of Ks for Two-Step spring

  Set \(x_{1}\), \(x_{2}\) as follows

  \[\begin{flalign} {{x}_{1}}=\frac{Fset}{Ks} && \end{flalign}\]
  \[\begin{flalign} {{x}_{2}}=\frac{Fset}{Ks} + \frac{{D}_{w}}{10} && \end{flalign}\]
  \[\begin{split}\begin{flalign} \left[ \begin{matrix} {x}_{1}^2 & {x}_{1} & 1 \\ {x}_{2}^2 & {x}_{2} & 1 \\ {2x}_{1} & 1 & 0 \end{matrix} \right] & \cdot \left\{ \begin{matrix} {a}_{s} \\ {b}_{s} \\ {c}_{s} \end{matrix} \right\} & = \left\{ \begin{matrix} {Fset} \\ 5Ksx_2 \\ Ks \end{matrix} \right\} && \end{flalign}\end{split}\]

  Using this, \(a_{s}\), \(b_{s}\), and \(c_{s}\) can be obtained

  Spring load for \(Ks\) becomes as follows,

  \(F=Ks \cdot x \ \ \ \ \ \ \ \ \ \ : x < x_{1}\)

  \(F=a_{s}x^2+b_{s}x+c_{s} \ \ \ \ \ \ : x_{1} \leq x\)

  

• Damping Coefficient

  \(C_{(x)} =C_0 \sqrt{\frac{K_{(x)}}{K_{(0)}}} : {C}_{0}={C}_{ps} \cdot 2 \cdot \sqrt{MK_1}\)

  Where,

  \(K_{(0)}\) is \(Ks\), \(Kh_{1}\), or \(Kh_{2}\) respectively.

  \(M\) = total mass, \(K_1\) = stiffness for free length

  \(C_{ps}\) = Damping Ratio (userinput)

Initial condition & position

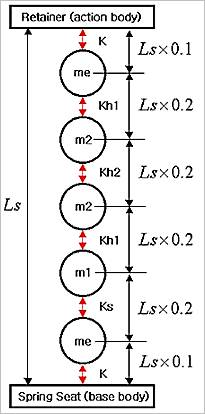
Figure 40.37 Initial Position

Total spring displacement is as below.

\({\delta}{L} = (Lf-Ls) +{\delta}{x}\)

Where,

\((Lf-Ls)\) is the displacement caused by set up.

\(\delta{x}\) is the displacement cause by cam-lift.

Displacement for each spring element \(x_j',(j=1,2,...,6)\), which caused by compression force, are obtained from spring characteristics. Because of the compression force is approximate value, there is the case that the sum of each displacement is not equal to the total displacement

\(\delta L \neq \sum _{j=1}^{6}{x}_{j}'\)

To minimize the error of displacement, following procedure is taken

\[\begin{flalign} {x}_{j}={x}_{j}'+\varepsilon \frac{{x}_{j}'}{\sum _{j=1}^{6}{x}_{j}'}, \varepsilon =\delta {L}-{\sum _{j=1}^{6}{x}_{j}'}&& \end{flalign}\]

where, \(\varepsilon ` is the total error and :math:`x_j\) is the corrected displacement of spring element.

The initial displacement of spring mass is the displacement from set up condition. So, the displacement of set up condition, \(x_{OSZY}\), should be subtracted from \(x_j\).

\(x_{OXZY}\) is obtained by setting the compression force equal to the \(Fset\).