10.9.1. RFlex Modal Force
The user can apply a user-defined load to a RFlex body using RFlex Modal Force. The function of RFlex Modal Force consists of three parts as Modal Load Case, Modal Force and Modal Preload.
Mathematical definitions
A set of nodal force and torque is can be translated to a generalized force with respect to the reference frame of RFlex body as following equation. The 3rd part of equation (10.24)
- Where,
- \({{\mathbf{F}}_{g}}\) is a generalized force with respect to the reference frame of RFlex body.\({{\mathbf{T}}_{g}}\) is a generalized torque with respect to the reference frame of RFlex body.\({{\mathbf{f}}_{g}}\) is a generalized modal force with respect to the reference frame of RFlex body.\({{\mathbf{F}}_{p}}\) is a force applied on \(p\) node with respect to the reference frame of RFlex body.\({{\mathbf{T}}_{p}}\) is a torque applied on \(p\) node with respect to the reference frame of RFlex body.\({{\mathbf{{d}'}}_{p}}\) is a position vector applied on \(p\) node with respect to the reference frame of RFlex body.\(\mathbf{\Phi }_{p}^{t}\) is a translational mode shape matrix. [3 \(\times\) nmode]\(\mathbf{\Phi }_{p}^{r}\) is a rotational mode shape matrix. [3 \(\times\) nmode]
If a force and torque a acting on the \(p\) node
The force vector including torque \({{\mathbf{F}}_{p}}\) [6 \(\times\) 1] is acting on the \(p\) node.
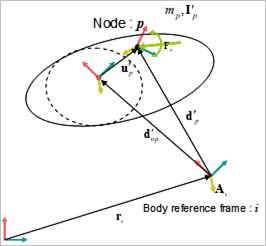
Figure 10.99 Simple example for Modal force
Therefore, we can write (10.25).
Where, \({{\mathbf{M}}_{p}}\) is a mass matrix [3 \(\times\) 3] on \(p\) node. \({{\mathbf{K}}_{p}}\) is a stiffness matrix [3 \(\times\) 3] on \(p\) node.
The \({{\mathbf{x}}_{p}}\) is defined as \({{\mathbf{\Phi }}_{p}}\mathbf{a}\). Where, \({{\mathbf{\Phi }}_{p}}\) is a mode shape matrix [6 \(\times\) nmode]. \(\mathbf{a}\) is modal coordinates.
Multiply \(\mathbf{\Phi }_{p}^{T}\) to (10.26)
Finally, we get a mathematical definition of Modal force as follows.